go-crypto-cipher

Go go crypto cipher
发布时间 :
字数:4.7k 阅读 :
  1. 非对称算法
    1. DSA
    2. RSA
    3. ECC
    4. ECC与RSA的比较
    5. ECIES
    6. ECDSA
  2. 对称加密算法
    1. CBC
    2. DES
    3. AES

  1. 非对称算法
    1. DSA
    2. RSA
    3. ECC
    4. ECC与RSA的比较
    5. ECIES
    6. ECDSA
  2. 对称加密算法
    1. CBC
    2. DES
    3. AES

非对称算法

非对称加密算法常用于数据加密和身份认证, 常见的非对称加密算法如下：

  • RSA: 由RSA公司发明，是一个支持变长密钥的公共密钥算法，需要加密的文件块的长度也是可变的；
  • DSA(Digital Signature Algorithm): 数字签名算法，是一种标准的DSS(数字签名标准)；
  • ECC(Elliptic Curves Cryptography): 椭圆曲线密码编码学。
  • ECDSA(Elliptic Curve Digital Signature Algorithm): 基于椭圆曲线的DSA签名算法

DSA

DSA是基于整数有限域离散对数难题的，其安全性与RSA相比差不多。DSA的一个重要特点是两个素数公开，这样，当使用别人的p和q时，即使不知道私钥，你也能确认它们是否是随机产生的，还是作了手脚。RSA算法却做不到
但是其缺点就是只能用于数字签名, 不能用于加密。

RSA

在1976年，由于对称加密算法已经不能满足需要，Diffie 和Hellman发表了一篇叫《密码学新动向》的文章，介绍了公匙加密的概念，由Rivet、Shamir、Adelman提出了RSA算法。
RSA是目前最有影响力的公钥加密算法，它能够抵抗到目前为止已知的绝大多数密码攻击，已被ISO推荐为公钥数据加密标准。

package main
import (
    "crypto/rand"
    "crypto/rsa"
    "crypto/sha1"
    "crypto/x509"
    "encoding/pem"
    "fmt"
)
// 使用对方的公钥的数据, 只有对方的私钥才能解开
func encrypt(plain string, publicKey string) (cipherByte []byte, err error) {
    msg := []byte(plain)
    // 解码公钥
    pubBlock, _ := pem.Decode([]byte(publicKey))
    // 读取公钥
    pubKeyValue, err := x509.ParsePKIXPublicKey(pubBlock.Bytes)
    if err != nil {
        panic(err)
    }
    pub := pubKeyValue.(*rsa.PublicKey)
    // 加密数据方法: 不用使用EncryptPKCS1v15方法加密,源码里面推荐使用EncryptOAEP, 因此这里使用安全的方法加密
    encryptOAEP, err := rsa.EncryptOAEP(sha1.New(), rand.Reader, pub, msg, nil)
    if err != nil {
        panic(err)
    }
    cipherByte = encryptOAEP
    return
}
// 使用私钥解密公钥加密的数据
func decrypt(cipherByte []byte, privateKey string) (plainText string, err error) {
    // 解析出私钥
    priBlock, _ := pem.Decode([]byte(privateKey))
    priKey, err := x509.ParsePKCS1PrivateKey(priBlock.Bytes)
    if err != nil {
        panic(err)
    }
    // 解密RSA-OAEP方式加密后的内容
    decryptOAEP, err := rsa.DecryptOAEP(sha1.New(), rand.Reader, priKey, cipherByte, nil)
    if err != nil {
        panic(err)
    }
    plainText = string(decryptOAEP)
    return
}
func test() {
    msg := "Content bo be encrypted!"
    // 获取公钥, 生产环境往往是文件中读取, 这里为了测试方便, 直接生成了.
    publicKeyData := `-----BEGIN PUBLIC KEY-----
MIGfMA0GCSqGSIb3DQEBAQUAA4GNADCBiQKBgQDZsfv1qscqYdy4vY+P4e3cAtmv
ppXQcRvrF1cB4drkv0haU24Y7m5qYtT52Kr539RdbKKdLAM6s20lWy7+5C0Dgacd
wYWd/7PeCELyEipZJL07Vro7Ate8Bfjya+wltGK9+XNUIHiumUKULW4KDx21+1NL
AUeJ6PeW+DAkmJWF6QIDAQAB
-----END PUBLIC KEY-----
`
    // 获取私钥
    privateKeyData := `-----BEGIN RSA PRIVATE KEY-----
MIICXQIBAAKBgQDZsfv1qscqYdy4vY+P4e3cAtmvppXQcRvrF1cB4drkv0haU24Y
7m5qYtT52Kr539RdbKKdLAM6s20lWy7+5C0DgacdwYWd/7PeCELyEipZJL07Vro7
Ate8Bfjya+wltGK9+XNUIHiumUKULW4KDx21+1NLAUeJ6PeW+DAkmJWF6QIDAQAB
AoGBAJlNxenTQj6OfCl9FMR2jlMJjtMrtQT9InQEE7m3m7bLHeC+MCJOhmNVBjaM
ZpthDORdxIZ6oCuOf6Z2+Dl35lntGFh5J7S34UP2BWzF1IyyQfySCNexGNHKT1G1
XKQtHmtc2gWWthEg+S6ciIyw2IGrrP2Rke81vYHExPrexf0hAkEA9Izb0MiYsMCB
/jemLJB0Lb3Y/B8xjGjQFFBQT7bmwBVjvZWZVpnMnXi9sWGdgUpxsCuAIROXjZ40
IRZ2C9EouwJBAOPjPvV8Sgw4vaseOqlJvSq/C/pIFx6RVznDGlc8bRg7SgTPpjHG
4G+M3mVgpCX1a/EU1mB+fhiJ2LAZ/pTtY6sCQGaW9NwIWu3DRIVGCSMm0mYh/3X9
DAcwLSJoctiODQ1Fq9rreDE5QfpJnaJdJfsIJNtX1F+L3YceeBXtW0Ynz2MCQBI8
9KP274Is5FkWkUFNKnuKUK4WKOuEXEO+LpR+vIhs7k6WQ8nGDd4/mujoJBr5mkrw
DPwqA3N5TMNDQVGv8gMCQQCaKGJgWYgvo3/milFfImbp+m7/Y3vCptarldXrYQWO
AQjxwc71ZGBFDITYvdgJM1MTqc8xQek1FXn1vfpy2c6O
-----END RSA PRIVATE KEY-----
`
    cipherData, err := encrypt(msg, publicKeyData)
    if err != nil {
        panic(err)
    }
    fmt.Printf("encrypt message: %x\n", cipherData)
    plainData, err := decrypt(cipherData, privateKeyData)
    if err != nil {
        panic(err)
    }
    fmt.Printf("decrypt message:%s\n", plainData)
}
func main() {
    test()
}

ECC

ECC是建立在基于椭圆曲线的离散对数的难度, 大概过程如下:

给定椭圆曲线上的一个点P，一个整数k，求解Q=kP很容易；给定一个点P、Q，知道Q=kP，求整数k确是一个难题。ECDH即建立在此数学难题之上

今天只有短的RSA钥匙才可能被强力方式解破。到2008年为止，世界上还没有任何可靠的攻击RSA算法的方式。只要其钥匙的长度足够长，用RSA加密的信息实际上是不能被解破的。但在分布式计算和量子计算机理论日趋成熟的今天，RSA加密安全性受到了挑战。

随着分解大整数方法的进步及完善、计算机速度的提高以及计算机网络的发展，为了保障数据的安全，RSA的密钥需要不断增加，但是，密钥长度的增加导致了其加解密的速度大为降低，硬件实现也变得越来越难以忍受，这对使用RSA的应用带来了很重的负担，因此需要一种新的算法来代替RSA。

1985年N.Koblitz和Miller提出将椭圆曲线用于密码算法，根据是有限域上的椭圆曲线上的点群中的离散对数问题ECDLP。ECDLP是比因子分解问题更难的问题，它是指数级的难度。

椭圆曲线算法因参数不同有多种类型, 这个网站列出了现阶段那些ECC是相对安全的:椭圆曲线算法安全列表, 而curve25519便是其中的佼佼者。

Curve25519/Ed25519/X25519是著名密码学家Daniel J. Bernstein在2006年独立设计的椭圆曲线加密/签名/密钥交换算法, 和现有的任何椭圆曲线算法都完全独立。
特点是：

  • 完全开放设计: 算法各参数的选择直截了当，非常明确，没有任何可疑之处，相比之下目前广泛使用的椭圆曲线是NIST系列标准，方程的系数是使用来历不明的随机种子 c49d3608 86e70493 6a6678e1 139d26b7 819f7e90 生成的，非常可疑，疑似后门；
  • 高安全性： 一个椭圆曲线加密算法就算在数学上是安全的，在实用上也并不一定安全，有很大的概率通过缓存、时间、恶意输入摧毁安全性，而25519系列椭圆曲线经过特别设计，尽可能的将出错的概率降到了最低，可以说是实践上最安全的加密算法。例如，任何一个32位随机数都是一个合法的X25519公钥，因此通过恶意数值攻击是不可能的，算法在设计的时候刻意避免的某些分支操作，这样在编程的时候可以不使用if ，减少了不同if分支代码执行时间不同的时序攻击概率，相反， NIST系列椭圆曲线算法在实际应用中出错的可能性非常大，而且对于某些理论攻击的免疫能力不高， Bernstein 对市面上所有的加密算法使用12个标准进行了考察， 25519是几乎唯一满足这些标准的 http://t.cn/RMGmi1g ；
  • 速度快: 25519系列曲线是目前最快的椭圆曲线加密算法，性能远远超过NIST系列，而且具有比P-256更高的安全性；
  • 作者功底深厚: Daniel J. Bernstein是世界著名的密码学家，他在大学曾经开设过一门 UNIX 系统安全的课程给学生，结果一学期下来，发现了 UNIX 程序中的 91 个安全漏洞；他早年在美国依然禁止出口加密算法时，曾因为把自己设计的加密算法发布到网上遭到了美国政府的起诉，他本人抗争六年，最后美国政府撤销所有指控，目前另一个非常火的高性能安全流密码 ChaCha20 也是出自 Bernstein 之手；
  • 下一代的标准: 25519系列曲线自2006年发表以来，除了学术界无人问津， 2013 年爱德华·斯诺登曝光棱镜计划后，该算法突然大火，大量软件，如OpenSSH都迅速增加了对25519系列的支持，如今25519已经是大势所趋，可疑的NIST曲线迟早要退出椭圆曲线的历史舞台，目前， RFC增加了SSL/TLS对X25519密钥交换协议的支持，OpenSSL 1.1也加入支持，是摆脱老大哥的第一步，下一步是将 Ed25519做为可选的TLS证书签名算法，彻底摆脱NIST

ECC与RSA的比较

ECC和RSA相比，在许多方面都有对绝对的优势，主要体现在以下方面：

  • 抗攻击性强。相同的密钥长度，其抗攻击性要强很多倍。
  • 计算量小，处理速度快。ECC总的速度比RSA、DSA要快得多。
  • 存储空间占用小。ECC的密钥尺寸和系统参数与RSA、DSA相比要小得多，意味着它所占的存贮空间要小得多。这对于加密算法在IC卡上的应用具有特别重要的意义。
  • 带宽要求低。当对长消息进行加解密时，三类密码系统有相同的带宽要求，但应用于短消息时ECC带宽要求却低得多。带宽要求低使ECC在无线网络领域具有广泛的应用前景。

ECC的这些特点使它必将取代RSA，成为通用的公钥加密算法。比如SET协议的制定者已把它作为下一代SET协议中缺省的公钥密码算法。

ECIES

ECDSA

因为在数字签名的安全性高, 基于ECC的DSA更高, 所以非常适合数字签名使用场景, 在SSH TLS有广泛使用, ECC把离散对数安全性高很少, 所以ECC在安全领域会成为下一个标准。

在golang的ssh库中就是使用这个算法来签名的: A使用自己的私钥签名一段数据, 然后将公钥发放出去. 用户拿到公钥后, 验证数据的签名,如果通过则证明数据来源是A, 从而达到身份认证的作用.

package main

import (
    "crypto/ecdsa"
    "crypto/elliptic"
    "crypto/md5"
    "crypto/rand"
    "fmt"
    "hash"
    "io"
    "math/big"
)
// SignData 用于保存签名的数据
type SignData struct {
    r         *big.Int
    s         *big.Int
    signhash  *[]byte
    signature *[]byte
}
// 使用私钥签名一段数据
func sign(message string, privateKey *ecdsa.PrivateKey) (signData *SignData, err error) {
    // 签名数据
    var h hash.Hash
    h = md5.New()
    r := big.NewInt(0)
    s := big.NewInt(0)
    io.WriteString(h, message)
    signhash := h.Sum(nil)
    r, s, serr := ecdsa.Sign(rand.Reader, privateKey, signhash)
    if serr != nil {
        return nil, serr
    }
    signature := r.Bytes()
    signature = append(signature, s.Bytes()...)
    signData = &SignData{
        r:         r,
        s:         s,
        signhash:  &signhash,
        signature: &signature,
    }
    return
}
// 校验数字签名
func verifySign(signData *SignData, publicKey *ecdsa.PublicKey) (status bool) {
    status = ecdsa.Verify(publicKey, *signData.signhash, signData.r, signData.s)
    return
}
func test() {
    //使用椭圆曲线的P256算法,现在一共也就实现了4种,我们使用折中一种,具体见http://golang.org/pkg/crypto/elliptic/#P256
    pubkeyCurve := elliptic.P256()
    privateKey := new(ecdsa.PrivateKey)
    // 生成秘钥对
    privateKey, err := ecdsa.GenerateKey(pubkeyCurve, rand.Reader)
    if err != nil {
        panic(err)
    }
    var publicKey ecdsa.PublicKey
    publicKey = privateKey.PublicKey
    // 签名
    signData, err := sign("This is a message to be signed and verified by ECDSA!", privateKey)
    if err != nil {
        panic(err)
    }
    fmt.Printf("The signhash: %x\nThe signature: %x\n", *signData.signhash, *signData.signature)
    // 验证
    status := verifySign(signData, &publicKey)
    fmt.Printf("The verify result is: %v\n", status)
}
func main() {
    test()
}

对称加密算法

对称加密算法用来对敏感数据等信息进行加密，常用的算法包括：

  • DES(Data Encryption Standard): 数据加密标准，速度较快，适用于加密大量数据的场合。
  • 3DES(Triple DES): 是基于DES，对一块数据用三个不同的密钥进行三次加密，强度更高。
  • AES(Advanced Encryption Standard): 高级加密标准，是下一代的加密算法标准，速度快，安全级别高
  • CBC 分组加密的四种模式之一(ECB、CBC、CFB、OFB)

对称加密又分为分组加密和序列密码。

  • 分组密码，也叫块加密(block cyphers)，一次加密明文中的一个块。是将明文按一定的位长分组，明文组经过加密运算得到密文组，密文组经过解密运算（加密运算的逆运算），还原成明文组。

  • 序列密码，也叫流加密(stream cyphers)，一次加密明文中的一个位。是指利用少量的密钥（制乱元素）通过某种复杂的运算（密码算法）产生大量的伪随机位流，用于对明文位流的加密。

CBC

分组密码，也叫块加密(block cyphers)，一次加密明文中的一个块。是将明文按一定的位长分组，明文组经过加密运算得到密文组，密文组经过解密运算（加密运算的逆运算），还原成明文组。
序列密码，也叫流加密(stream cyphers)，一次加密明文中的一个位。是指利用少量的密钥（制乱元素）通过某种复杂的运算（密码算法）产生大量的伪随机位流，用于对明文位流的加密。
解密是指用同样的密钥和密码算法及与加密相同的伪随机位流，用以还原明文位流

分组加密算法中，有ECB,CBC,CFB,OFB这几种算法模式, 我们介绍其中常用的一种CBC

CBC(Cipher Block Chaining)/密文分组链接方式

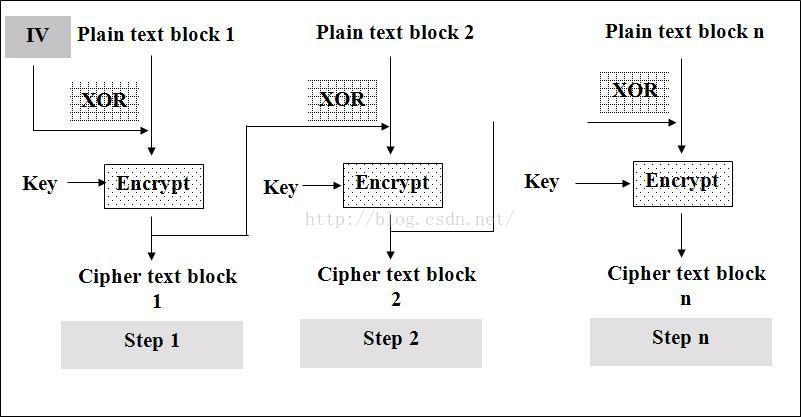
加密步骤如下：

  • 首先将数据按照8个字节一组进行分组得到D1D2……Dn（若数据不是8的整数倍，用指定的PADDING数据补位）
  • 第一组数据D1与初始化向量I异或后的结果进行DES加密得到第一组密文C1（初始化向量I为全零）
  • 第二组数据D2与第一组的加密结果C1异或以后的结果进行DES加密，得到第二组密文C2
  • 之后的数据以此类推，得到Cn
  • 按顺序连为C1C2C3……Cn即为加密结果。
// aesCBCEncrypt aes加密，填充秘钥key的16位，24,32分别对应AES-128, AES-192, or AES-256.
func aesCBCEncrypt(rawData, key []byte) ([]byte, error) {
    block, err := aes.NewCipher(key)
    if err != nil {
        return nil, err
    }

    //填充原文
    blockSize := block.BlockSize()
    rawData = pkcs7Padding(rawData, blockSize)
    //初始向量IV必须是唯一，但不需要保密
    cipherText := make([]byte, blockSize+len(rawData))
    //block大小 16
    iv := cipherText[:blockSize]
    if _, err := io.ReadFull(rand.Reader, iv); err != nil {
        return nil, err
    }

    //block大小和初始向量大小一定要一致
    mode := cipher.NewCBCEncrypter(block, iv)
    mode.CryptBlocks(cipherText[blockSize:], rawData)

    return cipherText, nil
}

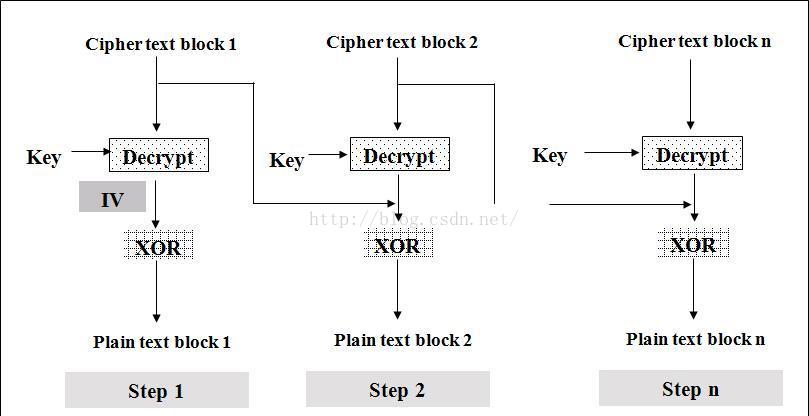
解密是加密的逆过程，步骤如下：

  • 首先将数据按照8个字节一组进行分组得到C1C2C3……Cn
  • 将第一组数据进行解密后与初始化向量I进行异或得到第一组明文D1（注意：一定是先解密再异或）
  • 将第二组数据C2进行解密后与第一组密文数据进行异或得到第二组数据D2
  • 之后依此类推，得到Dn
  • 按顺序连为D1D2D3……Dn即为解密结果。
func aesCBCDecrypt(encryptData, key []byte) ([]byte, error) {
    block, err := aes.NewCipher(key)
    if err != nil {
        return nil, err
    }

    blockSize := block.BlockSize()

    if len(encryptData) < blockSize {
        return nil, errors.New("ciphertext too short")
    }
    iv := encryptData[:blockSize]
    encryptData = encryptData[blockSize:]

    // CBC mode always works in whole blocks.
    if len(encryptData)%blockSize != 0 {
        return nil, errors.New("ciphertext is not a multiple of the block size")
    }

    mode := cipher.NewCBCDecrypter(block, iv)

    // CryptBlocks can work in-place if the two arguments are the same.
    mode.CryptBlocks(encryptData, encryptData)
    //解填充
    encryptData = pkcs7UnPadding(encryptData)
    return encryptData, nil
}

这里注意一点，解密的结果并不一定是我们原来的加密数据，可能还含有你补得位，一定要把补位去掉才是你的原来的数据。

特点：

  • 不容易主动攻击,安全性好于ECB,适合传输长度长的报文,是SSL、IPSec的标准。每个密文块依赖于所有的信息块, 明文消息中一个改变会影响所有密文块
  • 发送方和接收方都需要知道初始化向量
  • 加密过程是串行的，无法被并行化(在解密时，从两个邻接的密文块中即可得到一个平文块。因此，解密过程可以被并行化)。

DES

DES全称为Data Encryption Standard，即数据加密标准，是一种使用密钥加密的块算法，1977年被美国联邦政府的国家标准局确定为联邦资料处理标准（FIPS），并授权在非密级政府通信中使用，随后该算法在国际上广泛流传开来。

AES与3DES的比较:

算法名称 算法类型 密钥长度 速度 解密时间（建设机器每秒尝试255个密钥） 资源消耗
AES 对称block密码 128、192、256位 高 1490000亿年 低
3DES 对称feistel密码 112位或168位 低 46亿年 中 
破解历史
历史上有三次对DES有影响的攻击实验。1997年，利用当时各国 7万台计算机，历时96天破解了DES的密钥。1998年，电子边境基金会（EFF）用25万美元制造的专用计算机，用56小时破解了DES的密钥。1999年，EFF用22小时15分完成了破解工作。因此。曾经有过卓越贡献的DES也不能满足我们日益增长的需求了。

AES

2000年10月，NIST(美国国家标准和技术协会)宣布通过从15种侯选算法中选出的一项新的密匙加密标准。Rijndael被选中成为将来的AES。 Rijndael是在1999年下半年，由研究员Joan Daemen和Vincent Rijmen创建的。AES正日益成为加密各种形式的电子数据的实际标准。
并于2002年5月26日制定了新的高级加密标准 (AES) 规范。

算法原理

AES算法基于排列和置换运算。排列是对数据重新进行安排，置换是将一个数据单元替换为另一个。AES 使用几种不同的方法来执行排列和置换运算。
AES是一个迭代的、对称密钥分组的密码，它可以使用128、192 和 256 位密钥，并且用 128 位（16字节）分组加密和解密数据。与公共密钥密码使用密钥对不同，对称密钥密码使用相同的密钥加密和解密数据。通过分组密码返回的加密数据的位数与输入数据相同。迭代加密使用一个循环结构，在该循环中重复置换和替换输入数据。

综上看来AES安全度最高, 基本现状就是AES已经替代DES成为新一代对称加密的标准, 下面是Golang中AES使用的栗子

package main
import (
    "crypto/aes"
    "crypto/cipher"
    "fmt"
)
var commonIV = []byte{0x00, 0x01, 0x02, 0x03, 0x04, 0x05, 0x06, 0x07, 0x08, 0x09, 0x0a, 0x0b, 0x0c, 0x0d, 0x0e, 0x0f}
func encrypt(plainText string, keyText string) (cipherByte []byte, err error) {
    // 转换成字节数据, 方便加密
    plainByte := []byte(plainText)
    keyByte := []byte(keyText)
    // 创建加密算法aes
    c, err := aes.NewCipher(keyByte)
    if err != nil {
        return nil, err
    }
    //加密字符串
    cfb := cipher.NewCFBEncrypter(c, commonIV)
    cipherByte = make([]byte, len(plainByte))
    cfb.XORKeyStream(cipherByte, plainByte)
    return
}
func decrypt(cipherByte []byte, keyText string) (plainText string, err error) {
    // 转换成字节数据, 方便加密
    keyByte := []byte(keyText)
    // 创建加密算法aes
    c, err := aes.NewCipher(keyByte)
    if err != nil {
        return "", err
    }
    // 解密字符串
    cfbdec := cipher.NewCFBDecrypter(c, commonIV)
    plainByte := make([]byte, len(cipherByte))
    cfbdec.XORKeyStream(plainByte, cipherByte)
    plainText = string(plainByte)
    return
}
func main() {
    plain := "The text need to be encrypt."
    // AES 规定有3种长度的key: 16, 24, 32分别对应AES-128, AES-192, or AES-256
    key := "abcdefgehjhijkmlkjjwwoew"
    // 加密
    cipherByte, err := encrypt(plain, key)
    if err != nil {
        fmt.Println(err)
    }
    fmt.Printf("%s ==> %x\n", plain, cipherByte)
    // 解密
    plainText, err := decrypt(cipherByte, key)
    if err != nil {
        fmt.Println(err)
    }
    fmt.Printf("%x ==> %s\n", cipherByte, plainText)
}

©2024 Akabane71

Built with Hexo and 3-hexo theme

github